VECTORES

SEGMENTO: Dados dos puntos A y B del plano, se llama segmento de extremos A y B al conjunto de puntos de la recta que pasa por A y B que se encuentran comprendidos entre ellos. Le llamaremos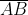 

SEGMENTO ORIENTADO: Si tenemos un segmento 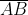 y establecemos un orden, es decir, identificamos cual de los puntos precede al otro, diremos que hemos orientado el segmento. Al primero de los puntos llamaremos ORIGEN (o punto de aplicación) y al último EXTREMO. (a un segmento orientado también se lo denomina vector fijo) y se lo representa poniéndole una flecha sobre las letras que lo representan .  Dado un segmento, existen dos posibles vectores fijos distintos  y 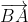. A la recta que contiene a los puntos A y B se la denomina recta directriz o de acción.

Dirección de un vector fijo: Llamaremos dirección de un vector fijo  a la dada por la recta que contiene a el segmento 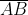 o a cualquiera de sus paralelas.

Sentido de vectores fijos: El sentido de un vector fijo está dado por su ORIGEN y su EXTREMO, como se mencionó antes, dado un segmento 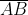, existen dos posibles vectores fijos distintos  y 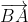, donde el sentido del primero es de A hacia B y el del segundo es de B hacia A.

Módulo de un vector fijo: Se llama Módulo de un vector fijo 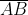 (se representa   ) al número real que representa la medida (longitud) del segmento  .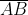

Vector nulo: A los vectores que tienen el origen coincidente con el extremo (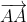) diremos que tienen módulo cero, y que no tienen dirección ni sentido.

Vectores Equipolentes: Dos vectores fijos (que no sean nulos) son equipolentes si tienen el mismo módulo, dirección y sentido. Para comprobarlo, se unen sus orígenes y sus extremos respectivos. Si el polígono resultante es un paralelogramo, los vectores son equipolentes.

(dos vectores nulos también se dice que son equipolentes)

Vectores libres del plano: Un vector libre del plano es un conjunto formado por infinitos vectores fijos equipolentes. Los vectores libres se denotan con letras minúsculas, por ejemplo . 

La gran ventaja de un vector libre es que podemos moverlo libremente por el plano, pues ahora ya no está sujeto a un origen y un extremo. Cada vez que lo movamos estaremos escogiendo un vector fijo distinto como representante del vector libre.

Un vector se puede definir por sus coordenadas, si un vector se encuentra en el plano se representa 
siendo sus componentes vx y vy ; la coordenada vx será igual al módulo del vector componente vx y la coordenada vy será igual al módulo del vector componente vy.

 

Siendo el vector la suma vectorial de sus vectores componentes:  

Suma de vectores.

Para sumar dos vectores libres  y  , debemos elegir dos vectores representantes tal que el origen del segundo vector coincida con el extremo del primero.
La suma de estos dos vectores será igual a otro vector, cuyo origen será el origen del primer vector, y el extremo será el extremo del segundo vector como se puede apreciar en la figura.

Este método es conocido como el Método de Chasles.

Existe otro método, al cual llamaremos Método del paralelogramo.

El cual consiste en tomar dos representantes de los vectores que vamos a sumar, tal que sus orígenes coincidan, luego por el extremo de cada vector se traza una paralela al otro vector, formando así un paralelogramo, la suma de los vectores será el vector con origen el punto de origen de ambos vectores (los cuales coinciden) y el extremo será el punto en donde se intersectan las paralelas que trazamos.

Vectores Opuestos: Los vectores opuestos son aquellos vectores que tienen igual dirección, igual módulo pero sentido opuesto.

                                          

Resta de vectores: Para restar dos vectores libres  y, debemos tomar un representante del vector  y sumarlo a un vector representante del opuesto del vector  . Este nuevo vector será el representante de la resta   - .

Multiplicación de un escalar por un vector: 

El resultado de la multiplicar un escalar k por un vector , es otro vector

• Con igual dirección que .
• Tendrá el mismo sentido que  si k es positivo, o tendrá sentido opuesto a  si k es negativo.
• El módulo será igual a  

Las coordenadas del nuevo vector, se obtienen de multiplicar k a las coordenadas del vector. Si , se cumple que   sería igual a 

Referencias: 
http://www.geoan.com/vectores/
http://es.wikipedia.org/wiki/Vector